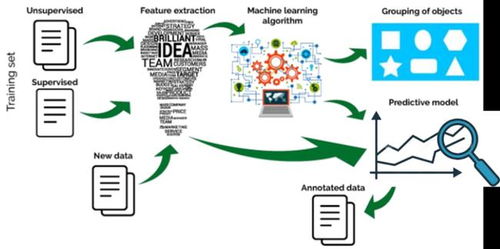
机器学习 回归算法,鏈樉绀洪闈紝鍥犱负璇锋眰瀹炰綋杩囧銆

机器学习中的回归算法是一种用于预测连续数值的预测方法。它通过建立输入特征和输出目标之间的数学关系，来预测未知数据点的数值。回归算法广泛应用于各种领域，如金融预测、房价预测、销量预测等。

回归算法的主要目标是找到一个函数，该函数能够最小化预测值与实际值之间的差异。这个函数通常是一个线性函数，但在某些情况下，可能需要使用非线性函数来更好地拟合数据。

以下是几种常见的回归算法：

1. 线性回归（Linear Regression）：线性回归是最基本的回归算法，它假设输入特征和输出目标之间存在线性关系。线性回归的目标是找到一个线性方程，使得预测值与实际值之间的差异最小。

2. 决策树回归（Decision Tree Regression）：决策树回归是一种基于决策树的回归算法。它通过递归地分割数据集，将数据集划分为更小的子集，并在每个子集上建立回归模型。决策树回归能够处理非线性关系，并且具有很好的解释性。

3. 随机森林回归（Random Forest Regression）：随机森林回归是一种基于决策树的集成学习算法。它通过构建多个决策树，并将它们的预测结果进行平均，来提高预测的准确性。随机森林回归能够处理非线性关系，并且对噪声数据具有很好的鲁棒性。

4. 支持向量回归（Support Vector Regression）：支持向量回归是一种基于支持向量机的回归算法。它通过找到一个超平面，使得预测值与实际值之间的差异最小。支持向量回归能够处理非线性关系，并且对噪声数据具有很好的鲁棒性。

5. 神经网络回归（Neural Network Regression）：神经网络回归是一种基于神经网络的回归算法。它通过构建一个多层神经网络，并使用反向传播算法来训练网络，从而实现回归预测。神经网络回归能够处理复杂的非线性关系，并且具有很好的泛化能力。

选择合适的回归算法取决于数据的特点和问题的需求。在实际应用中，通常需要通过交叉验证和调参来选择最佳的回归算法和模型参数。

机器学习回归算法：揭秘数据背后的规律

在当今数据驱动的时代，机器学习技术已经成为众多领域解决复杂问题的利器。其中，回归算法作为机器学习的重要分支，在预测和分析数据方面发挥着至关重要的作用。本文将深入探讨回归算法的基本概念、原理、类型以及在实际应用中的优势。

一、回归算法的基本概念

回归算法是一种用于预测连续值的机器学习算法。它通过建立因变量与自变量之间的数学模型，从而实现对未知数据的预测。回归算法广泛应用于金融、医疗、气象、社会科学等领域。

二、回归算法的原理

回归算法的核心思想是找到一组参数，使得模型对训练数据的拟合程度最高。具体来说，回归算法通过以下步骤实现：

收集数据：收集与预测目标相关的数据，包括自变量和因变量。

选择模型：根据数据特点选择合适的回归模型，如线性回归、多项式回归、岭回归等。

训练模型：使用训练数据对模型进行训练，得到一组参数。

预测：使用训练好的模型对未知数据进行预测。

三、回归算法的类型

根据回归模型的特点，可以将回归算法分为以下几类：

线性回归：假设因变量与自变量之间存在线性关系，通过最小二乘法求解参数。

多项式回归：将自变量进行多项式变换，建立非线性模型。

岭回归：在最小二乘法的基础上，引入正则化项，防止过拟合。

逻辑回归：虽然名为回归，但实际上是一种分类算法，用于解决二分类问题。

四、回归算法在实际应用中的优势

回归算法在实际应用中具有以下优势：

易于理解和实现：回归算法的原理简单，易于理解和实现。

预测精度高：回归算法能够对连续值进行准确预测。

适用范围广：回归算法适用于各种领域的数据分析。

可解释性强：回归算法的预测结果可以通过参数解释，便于理解。

五、回归算法的局限性

尽管回归算法在实际应用中具有诸多优势，但也存在一些局限性：

对异常值敏感：回归算法对异常值较为敏感，可能导致预测结果不准确。

对非线性关系处理能力有限：线性回归模型难以处理非线性关系。

对数据量要求较高：回归算法需要大量的训练数据才能获得较高的预测精度。

回归算法作为机器学习的重要分支，在预测和分析数据方面具有广泛的应用。了解回归算法的基本概念、原理、类型以及在实际应用中的优势，有助于我们更好地利用这一工具解决实际问题。在实际应用中，我们还需关注回归算法的局限性，以便选择合适的算法和策略。

机器学习回归算法在数据分析和预测领域具有重要作用。通过本文的介绍，相信读者对回归算法有了更深入的了解。在今后的学习和工作中，我们可以结合实际需求，灵活运用回归算法，为解决实际问题提供有力支持。